POLINOMIOS
En
matemáticas, un
polinomio (del
griego, πολυς
polys 'muchos' y νόμος
nómos 'regla, prescripción, distribución', a través del
latín polynomius)
[1] [2] [3] es una
expresión matemática constituida por un conjunto finito de
variables (
no determinadas o desconocidas) y
constantes (números fijos llamados
coeficientes), utilizando únicamente las
operaciones aritméticas de suma, resta y multiplicación, así como también
exponentes enteros positivos. En términos más precisos, es una
relación n-aria de
monomios, o una sucesión de sumas y restas de potencias enteras de una o de varias variables indeterminadas.
Es frecuente el término
polinómico (ocasionalmente también el anglicismo
polinomial), como adjetivo, para designar cantidades que se pueden expresar como polinomios de algún parámetro, como por ejemplo:
tiempo polinómico, etc.
Los polinomios son objetos muy utilizados en matemáticas y en ciencia. En la práctica, son utilizados en
cálculo y
análisis matemático para aproximar cualquier
función derivable; las
ecuaciones polinómicas y las funciones polinómicas tienen aplicaciones en una gran variedad de problemas, desde la matemática elemental y el
álgebra hasta áreas como la
física,
química,
economía y las
ciencias sociales.
En áreas de las
matemáticas aplicadas, los polinomios son utilizados para construir los
anillos de polinomios, un concepto central en
álgebra abstracta y
geometría algebraica.
Para
a0, …,
an constantes en algún
anillo A (en particular podemos tomar un
cuerpo, como

o

, en cuyo caso los coeficientes del polinomio serán números) con
an distinto de cero y

, entonces un polinomio,

, de grado
n en la variable
x es un objeto de la forma
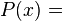

El polinomio se puede escribir más concisamente usando
sumatorios como

Las constantes
a0, …,
an se llaman los
coeficientes del polinomio. A
a0 se le llama el
coeficiente constante (o término independiente) y a
an, el
coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normalizado.
Los polinomios de varias variables, a diferencia de los de una variable, tienen en total más de una variable. Por ejemplo los monomios:
-

En detalle el último de ellos
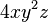
es un monomio de tres variables (ya que en él aparecen las tres letras
x,
y y
z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de
x,
y y
z respectivamente.
Se define el grado de un
monomio como el mayor exponente de su variable. El grado de un polinomio es el del monomio de mayor grado.
- Ejemplos
- P(x) = 2, polinomio de grado cero (el polinomio solo consta del término independiente).
- P(x) = 3x + 2, polinomio de grado uno.
- P(x) = 3x² + 2x², polinomio de grado dos.
- P(x) = 2x3+ 3x + 2, polinomio de grado tres.
Convencionalmente se define el grado del polinomio nulo como

. En particular los números son polinomios de grado cero.
Los polinomios se pueden
sumar y
restar agrupando los términos y simplificando los
monomios semejantes. Para multiplicar polinomios se multiplica cada término de un polinomio por cada uno de los términos del otro polinomio y luego se simplifican los monomios semejantes.
- Ejemplo
Sean los polinomios:

y

, entonces el producto es:





Para poder realizar eficazmente la operación se tiene que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:



Aplicando esta fórmula al ejemplo anterior se tiene:




Puede comprobarse que para polinomios no nulos se satisface la siguiente relación entre el grado de los polinomios

y

y el polinomio producto

:
(*)

Puesto que el producto de cualquier polinomio por el polinomio nulo es el propio polinomio nulo, se define convencionalmente que

(junto con la operación

) por lo que la expresión (
*) puede extenderse también al caso de que alguno de los polinomios sea nulo.
Una
función polinómica es una
función matemática expresada mediante un polinomio. Dado un polinomio
P[
x] se puede definir una función polinómica asociada al polinomio dado substituyendo la variable
x por un elemento del anillo:

La funciones polinómicas reales son
funciones suaves, es decir, son infinitamente diferenciables (tienen derivadas de todos los órdenes). Debido a su estructura simple, las funciones polinómicas son muy sencillas de evaluar numéricamente, y se usan ampliamente en
análisis numérico para
interpolación polinómica o para
integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la
regla de Horner.
En
álgebra lineal el
polinomio característico de una
matriz cuadrada codifica muchas propiedades importantes de la
matriz. En
teoría de los grafos el
polinomio cromático de un
grafo codifica las distintas maneras de colorear los vértices del grafo usando
x colores.
Con el desarrollo de la
computadora, los polinomios han sido remplazados por funciones
spline en muchas áreas del análisis numérico. Las splines se definen a partir de polinomios y tienen mayor flexibilidad que los polinomios ordinarios cuando definen funciones simples y suaves. Éstas son usadas en la
interpolación spline y en gráficos por
computadora.
Note que las gráficas representan a las
funciones polinomiales y no a los polinomios en sí, pues un polinomio solo es la suma de varios monomios.

Polinomio de grado 2: f( x) = x2 - x - 2= ( x+1)( x-2).
|
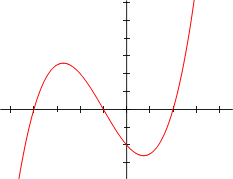
Polinomio de grado 3: f( x) = x3/5 + 4 x2/5 - 7 x/5 - 2= 1/5 ( x+5)( x+1)( x-2).
|

Polinomio de grado 4: f( x) = 1/14 ( x+4)( x+1)( x-1)( x-3) + 0.5.
|

Polinomio de grado 5: f( x) = 1/20 ( x+4)( x+2)( x+1)( x-1)( x-3) + 2.
|
La función
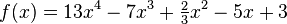
es un ejemplo de función polinómica de cuarto grado, con coeficiente principal 13 y una constante de 3.
En un
anillo conmutativo 
una condición necesaria para que un monomio sea un factor de un polinomio de grado
n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:


necesariamente

divide a

En caso de que el polinomio no tenga término independiente se sacará la incógnita como factor común y ya está factorizado. También se puede factorizar usando las igualdades notables.
Un polinomio factoriza dependiendo del anillo sobre el cual se considere la factorización, por ejemplo el
binomio 
no factoriza sobre

pero sí factoriza sobre

:

Por otra parte

no factoriza ni sobre

, ni tampoco sobre

aunque factoriza sobre

:

Un cuerpo en el que todo polinomio no constante factoriza en monomios es un
cuerpo algebraicamente cerrado.
 o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio,
, entonces un polinomio,  , de grado n en la variable x es un objeto de la forma
, de grado n en la variable x es un objeto de la forma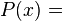



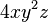 es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente. . En particular los números son polinomios de grado cero.
. En particular los números son polinomios de grado cero. y
y  , entonces el producto es:
, entonces el producto es:








 y
y  y el polinomio producto
y el polinomio producto  :
:
 (junto con la operación
(junto con la operación  ) por lo que la expresión (
) por lo que la expresión (




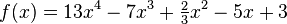
 una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:
una condición necesaria para que un monomio sea un factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:

 divide a
divide a 
 no factoriza sobre
no factoriza sobre  pero sí factoriza sobre
pero sí factoriza sobre 
 no factoriza ni sobre
no factoriza ni sobre  :
: